Künstliche Intelligenz
Die schnell voranschreitende Entwicklung der Künstlichen Intelligenz (KI) als Schlüsseltechnologie und deren Verfügbarkeit in Form von Bibliotheken für Programmierer bietet erhebliches Potenzial für die ZfP. Die intelligente Extraktion des verfolgten Informationsgehaltes aus Messdaten stellt einen entscheidenden Schlüssel zur Lösung von Prüfaufgaben dar. Einen dementsprechend hohen Stellenwert besitzen leistungsfähige Algorithmen und speziell die Einbeziehung von KI zur Datenanalyse. Neben der Erarbeitung KI-basierter ZfP-Lösungen wird KI als Methode der Analyse und des wissenschaftlichen Erkenntnisgewinns herangezogen.
Kontakt

Künstliche Intelligenz
Die schnell voranschreitende Entwicklung der Künstlichen Intelligenz (KI) als Schlüsseltechnologie und deren Verfügbarkeit in Form von Bibliotheken für Programmierer bietet erhebliches Potenzial für die ZfP. Die intelligente Extraktion des verfolgten Informationsgehaltes aus Messdaten stellt einen entscheidenden Schlüssel zur Lösung von Prüfaufgaben dar. Einen dementsprechend hohen Stellenwert besitzen leistungsfähige Algorithmen und speziell die Einbeziehung von KI zur Datenanalyse. Neben der Erarbeitung KI-basierter ZfP-Lösungen wird KI als Methode der Analyse und des wissenschaftlichen Erkenntnisgewinns herangezogen.
Ein eigenes Software Tool für die Konzipierung von KI-Lösungen ist mit Echolyst A.I. entstanden. Dabei handelt es sich um ein Deep Learning-Modul, welches an die Software Echolyst anknüpft .Die Entwicklung folgte dem Ziel ein praxistaugliches Werkzeug bereitzustellen, welches eine nutzerfreundliche Verwendung von Deep Learning ermöglicht.
Exemplarisch sei hier die Anwendung von Deep Learning in einer Regressionsaufgabe beschrieben. Dafür sei die klassische Anwendung des Impakt-Echo-Verfahrens zur Dickenmessung angeführt. Die Einschränkungen des Verfahrens hinsichtlich des Einflusses von Randeffekten bei kompakten Bauteilgeometrien sind im Beispiel deutlich erkennbar. Dabei handelt es sich um Messungen, welche am Florida Department of Transportation an einem Testkörper mit den Abmessungen 2.10 m x 1.50 m und Bereichen unterschiedlicher Dicke durchgeführt wurden. Während die klassische Auswertung einzig anhand der dominanten Frequenz sich bei weitgestreckten plattenartigen Bauteilen als robust erweist, führt sie im vorliegenden Fall aufgrund der starken Randeffekte nur zu unbefriedigenden Ergebnissen.
![Testkörper am Florida Department of Transportation [3] mit Feldern unterschiedlicher Dicke zur Untersuchung von Dickenmessverfahren.](https://www.svti.ch/sites/default/files/styles/auto_fit_max-w_300/public/2021-12/Abbildung_01_0.jpg?itok=qS7xgI99)
Testkörper am Florida Department of Transportation [3] mit Feldern unterschiedlicher Dicke zur Untersuchung von Dickenmessverfahren.
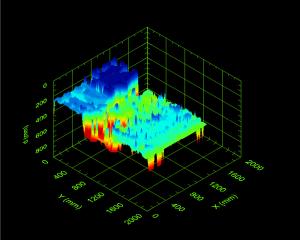
Dickenprofildarstellung als unbefriedigendes Ergebnis der klassischen Auswertung einzig anhand der dominanten Frequenz.
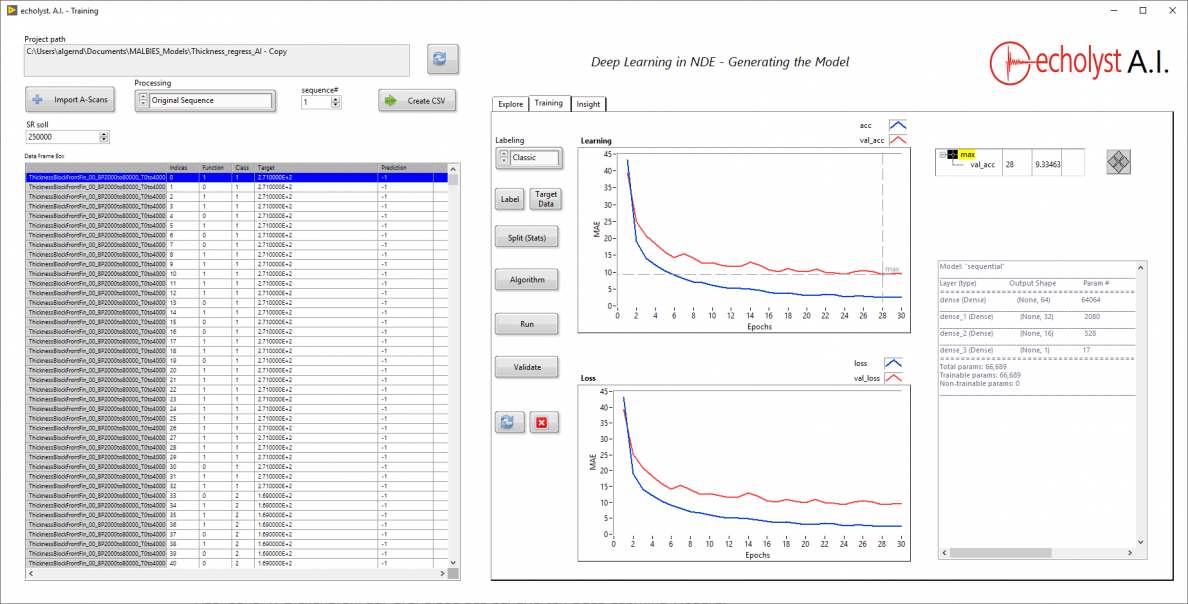
Neuronale Netze sind in der Lage, den gesamten Informationsgehalt von Datensätzen zu nutzen und leistungsfähige empirische Modelle zu generieren. So zeigt sich im vorliegenden Fall, dass sich ein Modell generieren lässt, welches eine deutlich höhere Genauigkeit als die klassische Auswertung aufweist. In der Abbildung als Lernkurve ist der über den Verlauf der Lernepochen erzielte mittlere Fehler (Mean Absolute Error) in mm dargestellt.
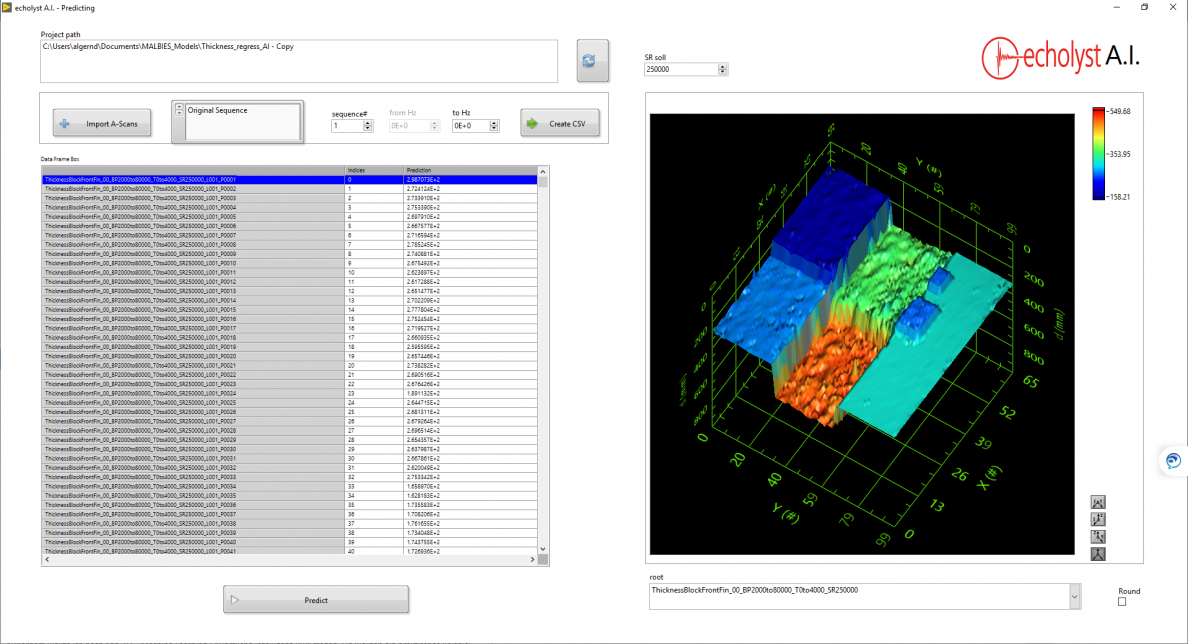
Das durch das generierte Modell ermittelte Ergebnisbild zeigt die unterschiedlichen Felder des Testkörpers deutlich. Dieses sollte als Demonstration verstanden werden, keineswegs wurde hier ein allgemeingültiges Modell generiert.